Trees

Trees and their immediate generalization, forests, are useful for any system that manipulates hierarchically organized information. The range of applications is broad, from abstract syntax trees in compilers through document structures in text processing systems to company organization charts in business software.
Trees, in particular binary trees and their variants, also provide convenient implementations of container data structures.

Basic Terminology

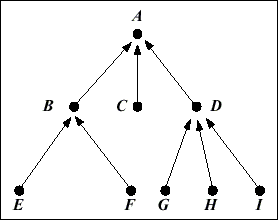
A tree consists of a set of nodes. Each node may have zero or more children, other nodes of which it is the parent. Each node has at most one parent, although it may have an arbitrary number of children.

A node with no parent, such as the node marked A on the figure, is called a root; a node with no children, such as E, F, G, H and I, is called a leaf. The length of a path from the root to a leaf (that is to say, the number of nodes on the path minus one) is the height of the tree; the average length of all such paths is the average height. On the figure the height is 2 and the average height is 11/6 since of the six paths five have length 2 and one has length 1.
The children of a common node are called siblings. For example G, H and I are siblings on the figure. The siblings of a node are usually considered to be ordered; the order corresponds to the direction from left to right on conventional figures such as this one.
The descendants of a node are the node itself and, recursively, the descendants of its children. The ancestors of a node are the node itself and, recursively, the ancestors of its parent. For example the descendants of A are all the tree’s nodes; and the ancestors of I are A, D and I.
To obtain a tree rather than a more general kind of graph, there is an extra requirement: in we start from an arbitrary node, go to the parent, to the parent’s parent and so on (for as long as there is a parent), we will never find the starting node again. In more precise terms the condition is that the “parent” relation must not have any cycles. (That relation is in fact a partial function, since every node has zero or one parent.) If we consider infinite as well as finite trees the above condition must be restated to express that if we start from an arbitrary node and repeatedly go to the parent we will eventually hit a root. This discussion, however, will only consider finite trees (those with a finite number of nodes), for which the two statements are equivalent.
The definition given so far properly defines forests rather than trees. A tree is a forest with at most one root (that is to say, with exactly one root unless it is empty), such as the example on the last figure. The discussion and the library classes will handle trees rather than forest, but this is not a very important difference since by using an obvious device you can treat any forest as a tree: simply add an extra node, and make it the parent of all the forest’s roots.
Another important observation is that there is a one-to-one correspondence between trees and nodes. To any node N of a tree T we can associate a tree: take T, remove all nodes that are not descendants of N, and use N as the new root. Conversely, to any tree we can associate a node - its root. This correspondence enables us to treat the two concepts of tree and node as essentially the same.

Recursive Trees

The closeness of the notions of tree and node yields an elegant definition of trees in terms of lists. If we look at trees or, equivalently, at tree nodes, we can consider each node as being both:

A list: the list of its children.
A list cell (similar to a LINKABLE or BI_LINKABLE for one-way and two-way linked lists), paired with the node’s siblings.

This yields a simple definition of trees by multiple inheritance from LIST and CELL.

Dynamic recursive trees

An example of dynamic tree structure is provided by class TWO_WA Y_TREE, an heir of both TWO_WAY_LIST and BI_LINKABLE. There is also LINKED_TREE, which inherits from LINKED_LIST and LINKABLE, but TWO_WA Y_TREE is generally preferable since children of a node often needs to be traversed both ways; the notion of order is usually less significant here than for lists. Such a form of definition is a particularly effective way of conveying the profoundly recursive nature of trees. The corresponding classes are useful in many different areas such as graphics, text processing and compilation. To create a one-way or two-way linked tree, use

create my_tree.make (root_value)

This will attach my_tree to a new one-node tree, with root_value at the root node. Here my_tree must be declared of type TWO_WA Y_TREE [MY_TYPE] for some type MY_TYPE, and root_value must be of type MY_TYPE.
A class with a similar interface but using arrays rather than lists to represent nodes is also available: ARRAYED_TREE . This class is more efficient in both time and space for trees whose nodes have many children that are accessed randomly, if relatively few child insertions occur after node creation. Here the creation procedure indicates the initial number of children:

create my_tree.make (max_estimated_children, root_value)

The integer argument max_estimated_children only serves for the initial allocation; the array will be resized if the number of children grows beyond the initial size. As with the previous kinds of tree, the newly created node initially has no children.

Fixed trees

TWO_WA Y_TREE is useful for fully dynamic trees, in which a node may get new children at any time. For some applications, the number of children of a tree, although still arbitrary, is set for each node when the node is created, and will not change after that. Of course, some children may be absent; the corresponding entries will be void references. Class FIXED_TREE provides the basic mechanism; as you may have guessed, the implementation associates with each node an array of its children, arrays usually being the right structure when a collection of objects is known not to change size after creation. To create a fixed tree, use

create my_tree.make (how_many_children, root_value)

The root will have the associated value root value and will have how_many_ children children, all initially void. Unlike the argument max_estimated_children for the creation procedure of ARRAYED_TREE , the value of how_many_children is the final arity of the newly created node; since it set separately for each node on creation, the various nodes of a tree can have different arities, as illustrated on the above figure.

Properties of recursive trees

Whether fixed or dynamic, recursive trees fully enjoy their dual origin. This means in particular that each node is viewed as a list of its children, and can apply to this list the features inherited from LIST, appropriately renamed; for example:
child_put_left
child_forth
child_put
and so on. Feature count, inherited from LIST, indicates the number of children; it is renamed arity to conform to accepted tree terminology. (The word is a substantived form of the “ary” adjective ending, as in “ternary”, “quaternary” and so on, which yielded the expression “n-ary”.)

BINARY TREES

Binary trees are a special case of fixed trees in which nodes always have two children, although either or both of these children may be void.

Basic binary trees

Class BINARY_TREE describes binary trees.

The children are represented by features left_childand right_child. Queries has_left and has_right indicate whether any of these is non-void; arity is redefined to yield the number of non-void children (0, 1 or 2).

Binary representations of trees

For any ordinary tree, there exists a standard representation as a binary tree, which is useful in some applications. The correspondence is one-to-one, so that the original tree may be reconstructed without ambiguity. It actually applies to forests rather than trees and works as follows, fr being the first root in a forest: the binary tree’s root corresponds to fr; its left subtree is obtained recursively from the forest made by the subtrees of fr; and its right subtree is obtained recursively from the original forest deprived of the tree rooted at fr. If you start from a tree rather than a forest the binary tree’s root will have no right child.
Function binary_representation, in TREE, creates a binary tree representation (the function’s result) obtained from the current tree.
Procedure fill_ from_binary, in DYNAMIC_TREE, reconstructs a tree from a binary tree representation passed as argument.

Binary search trees

Class BINARY_SEARCH_TREE describes binary search trees, an implementation of bags which is appropriate for comparable items.
Binary search trees rely for insertion on a policy whereby any item less than the root is inserted (recursively) into the left subtree, and any item greater than the root into the right subtree. So if the insertion order is reasonably random the items will distribute evenly among the various branches, This means that the average height of the tree will be not much more than the optimal: [log2 n] where n is the number of nodes and [x], for any x, is the integer part of x.
Since search operations will follow the same principle (search left if smaller than the root, and so on), the time to find an item or ascertain that it is not there is proportional to the average height. In normal cases this means about [log2 n] basic operations, rather than n with a linear structure such as a list, and hence much better performance for large n.

CURSOR TREES

Recursive trees, as described so far, are not active data structures: even though each node has its own cursor to traverse the list of its children, there is no global cursor on the tree as a whole. It is not hard to see that the notion of recursive tree is in fact incompatible with the presence of a global cursor. In situations where you need such a cursor, enabling you to move freely from a node to its children, siblings and parents, you may use class CURSOR_TREE and its descendants.

The conceptual model

With cursor trees the model is different from what we have seen earlier in this chapter: there is a clear distinction between the nodes and the tree itself. The manipulated object is a tree, and the notion of node is merely implicit. In the various operations presented below and illustrated on the following figure, “up” means towards the root and “down” towards the leaves. This, of course, is the reverse of the properties of trees of the other kind - those which grow towards the sun and serve to print books about software.

Operations on cursor trees

The cursor supported by instances of CURSOR_TREE has a position referring to a node of the tree, which is then considered to be the active node, or is off the tree. The different off positions are: above (above the root), below (below a leaf), before (before a leftmost sibling), after (after a rightmost sibling.) As with linear structures, fictitious sentinel elements are assumed to be present to the left, right, top and bottom.
Various procedures are available to move the cursor in all directions:

down (i) moves the cursor down to the i-th child of the active node. If i is equal to 0 the cursor ends up before; if i is equal to the arity of the current parent plus 1, the cursor ends up after. Calling down (i) when the cursor is on a leaf node results in setting below and before to true if i is equal to 0, or below and after to true if i is equal to arity+1.
forth and back move the cursor forward and backward between siblings and can cause the cursor to end up after or before.
up moves the cursor up one level. The call may be made even when the cursor is after or before. If the cursor is on the root of the tree or below in an empty tree, the cursor ends up above.

You can move the cursor in any one direction ( up, down, forth, back), repeatedly, until it is off (above, below, after, before respectively), but once it is off, further movement in the same direction is prohibited. For example the precondition of put_left requires before to be false, and the precondition of put_right requires after to be false.
It is possible to move down from an above position; in an empty tree this brings the cursor below. Similarly, it is possible to move up from below, left from after, right from before.
The sentinel element above the tree’s root is considered to be the root of a forest containing just one tree. This view justifies the convention for the result of arity when the cursor is above: 0 if the tree is_empty, 1 if it has a root (viewed as the child of the fictitious sentinel element).

Manipulating the cursor explicitly

The cursor attached to a cursor tree is not just a conceptual notion but an actual object, of type CURSOR. You may use the query cursor to obtain a reference to the current cursor. Procedure go_to takes a cursor as argument and brings the tree’s cursor to the node identified by the value of that argument.

Traversals

A useful notion associated with trees and particularly applicable to cursor trees is that of traversal.
A traversal is a certain policy for ordering all the nodes in a tree - usually to apply an operation to all these nodes in the resulting order. CURSOR_TREE and its descendants support three forms of traversal: preorder, postorder and breadth-first. They correspond to the most commonly used traversal policies on trees, illustrated on the figure (where the children of each node are assumed to be ordered from left to right):

Preorder is the traversal that visits the root first, then (recursively) traverses each subtree in order. On the figure we will visit node A first then, recursively, the subtrees rooted at B (which implies visiting E and F), C and D. The resulting order is: A B E F C D G H I.
Postorder first traverses (recursively) the subtrees, then visits the root. On the example this gives: E F B C G H I D A.
Breadth-first visits the nodes level by level, starting with the root: first the root, then all its children, then all their children and so on. Here the resulting order is: A B C D E F G H I.

For each of the traversals, procedures are available to move the cursor accordingly, for example breadth_start and breadth_ forth for breadth-first, and similar names for the others.